数据处理
数据处理是使用 LCDA 分析实验数据的关键部分。因为你收集的数据可能会存在一些问题,譬如存在噪声、偏斜等问题,所以在进行数据分析之前,需要对数据进行处理。
本章节将介绍数据处理的步骤。无论您是新手还是有经验的用户,我们希望本章节能够为您提供有用的信息和指导,以便您能够使用 LCDA 获得准确可靠的结果。
数据处理项目
新建项目
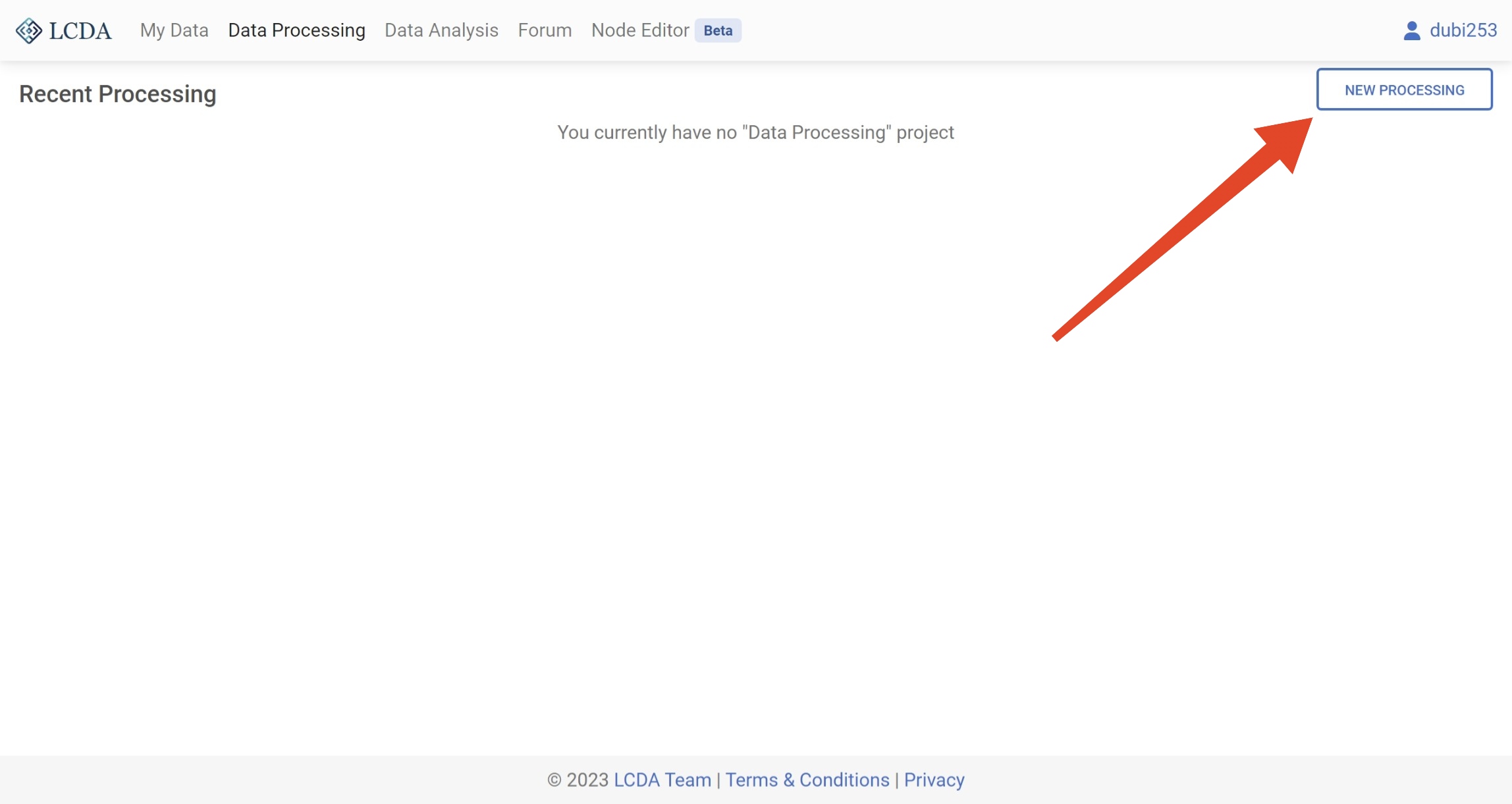
在开始数据处理之前,需要新建一个数据处理项目。 您可以通过单击 Data Processing 界面右上角的 NEW PROCESSING 按钮来新建一个数据处理项目。
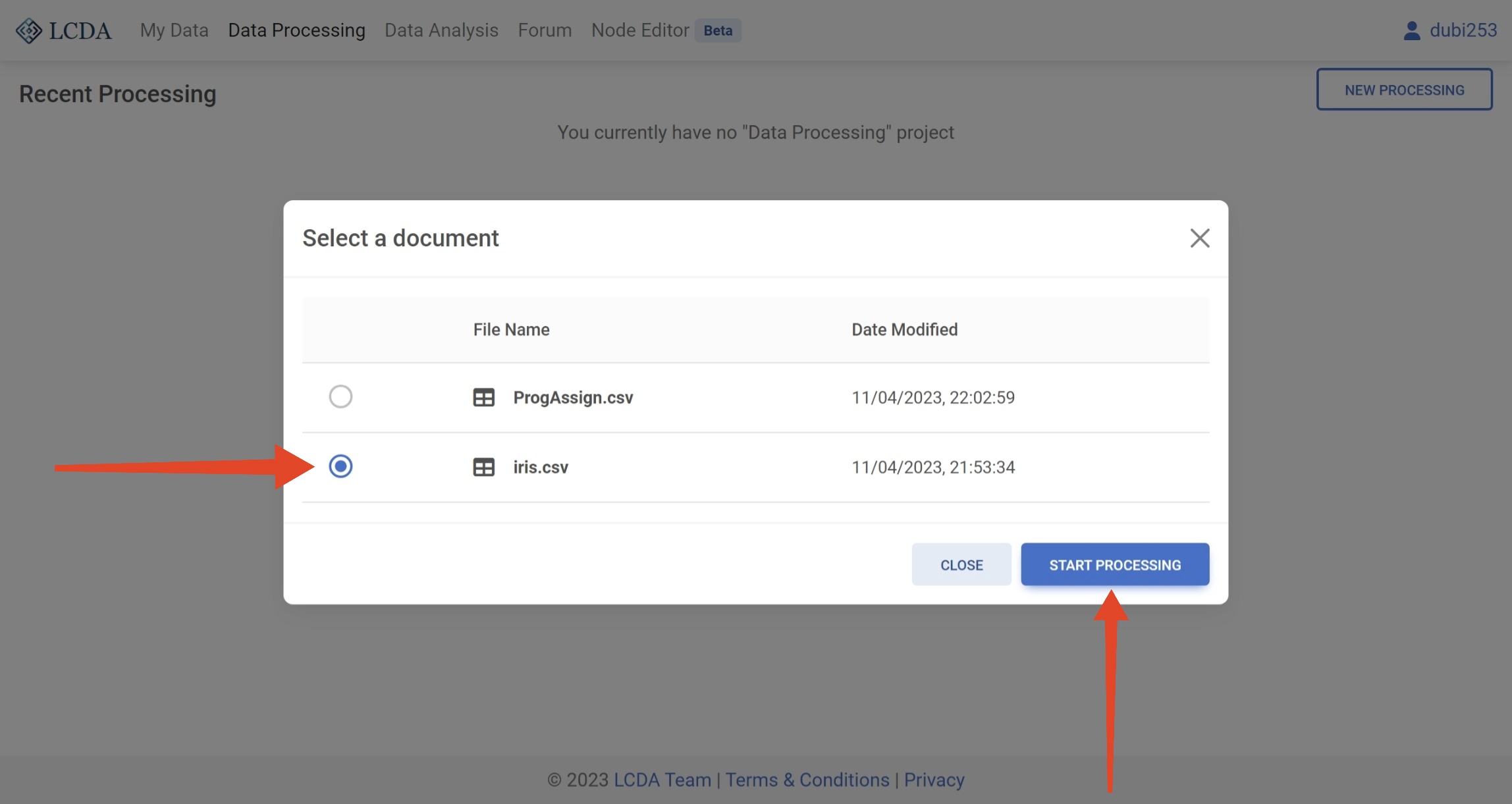
在弹出的界面中,您需要选择一个数据集(想要选择您自己的数据集? 请参考 My Data 用户手册查看如何上传数据集)。然后点击右下角的 START PROCESSING 按钮来开始数据处理。 系统会自动为您创建一个数据处理项目。
这里我们使用 iris.csv 数据集来演示数据处理的过程。
继续编辑项目
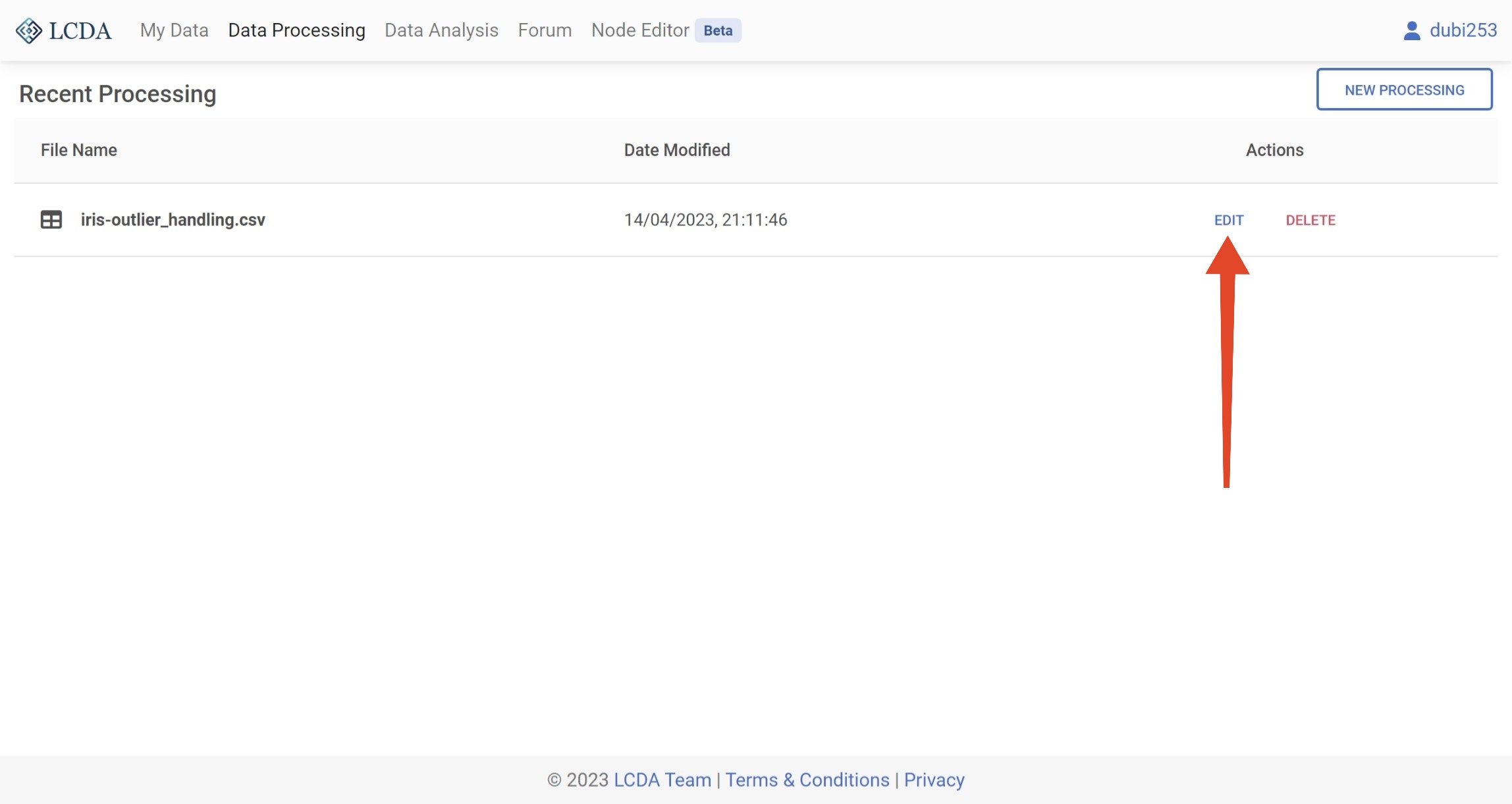
如果您已经创建了一个数据处理项目,则数据处理界面会列出您所有的数据处理项目。您可以通过单击右侧的 EDIT 按钮来继续编辑已有的数据处理项目。
删除项目
如果您不再需要某个数据处理项目,您可以通过单击右侧的 DELETE 按钮来删除该项目。
注意
注意:删除数据处理项目是永久性的操作,删除后无法恢复。这也会删除该项目中最后一次运行生成的数据集。
数据处理步骤
单击
EDIT按钮或创建新数据处理项目后,会显示数据处理界面。在这里,您可以对数据进行处理。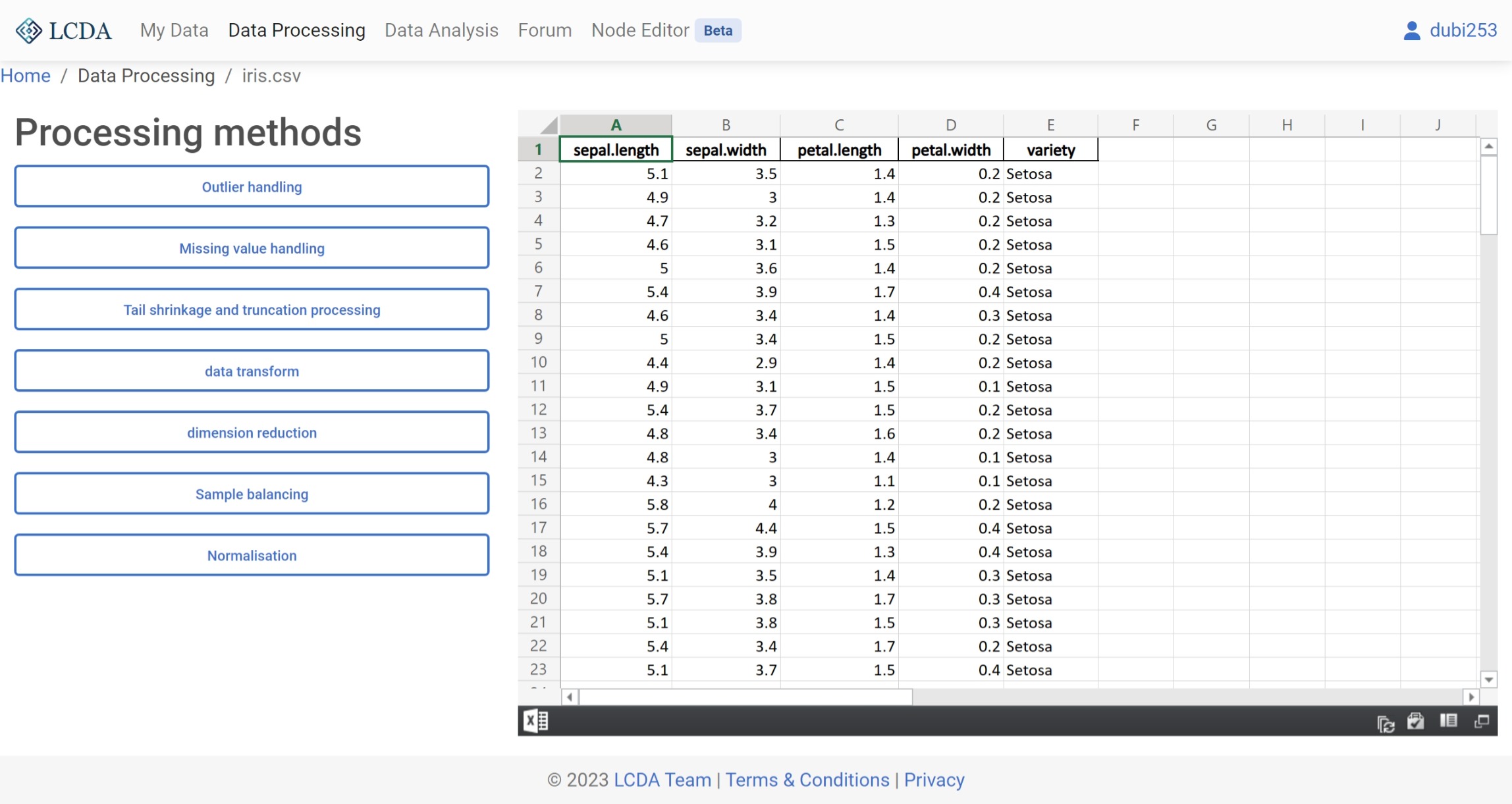
在数据处理界面中,您可以在左侧看到数据处理算法的列表。您可以通过单击左侧的算法来选择要使用的算法,并在弹出的面板中设置算法的参数。每种算法的具体参数可能会有所不同,因此请参阅数据处理算法介绍 以获取有关如何设置它们的更多信息。
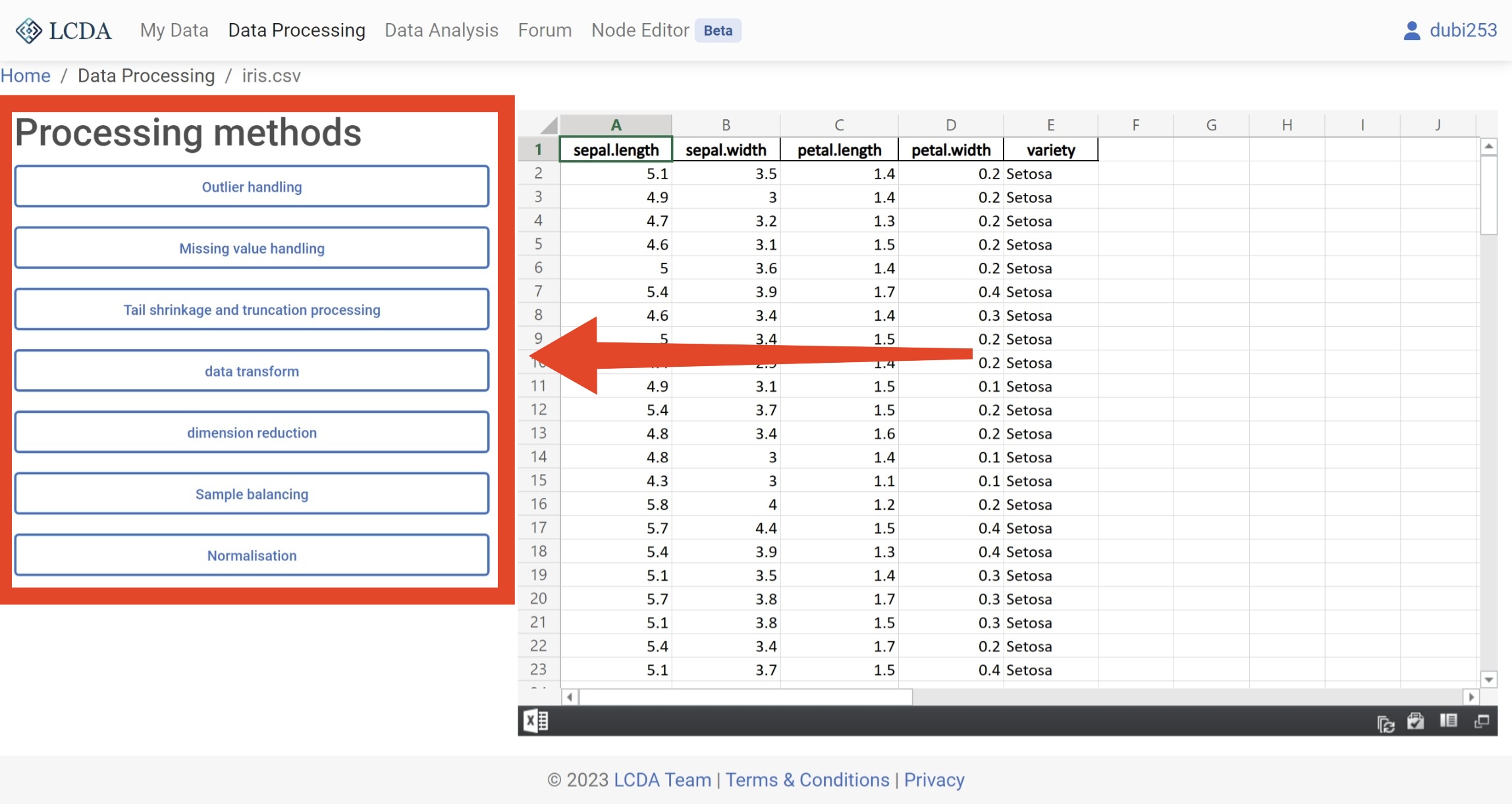
这里我们使用
Outlier handling算法举例。在选择好参数后,您可以单击面板右下角的Start processing按钮来运行算法。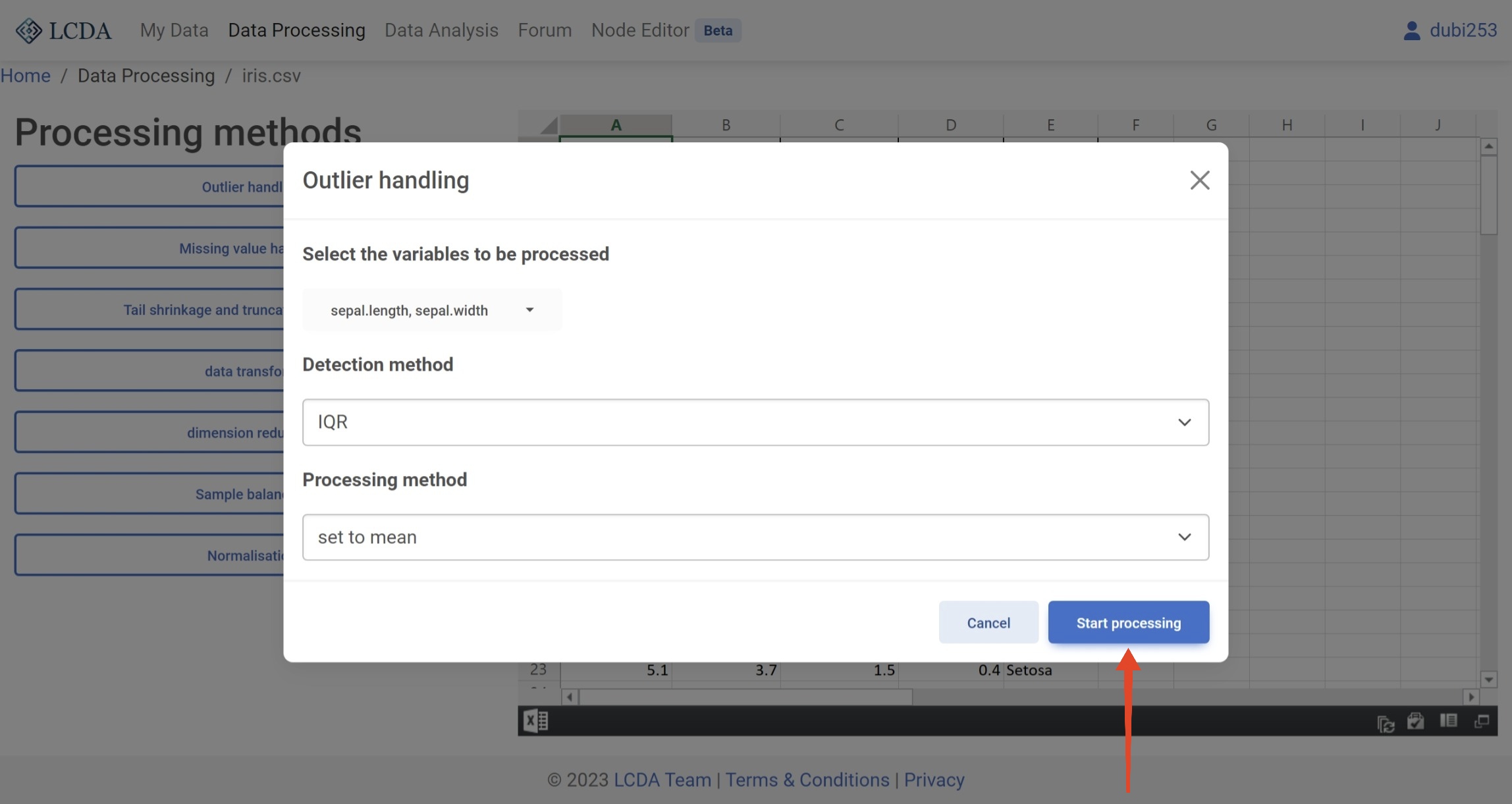
等待算法运行完成后,您可以在右侧看到算法的输出结果。
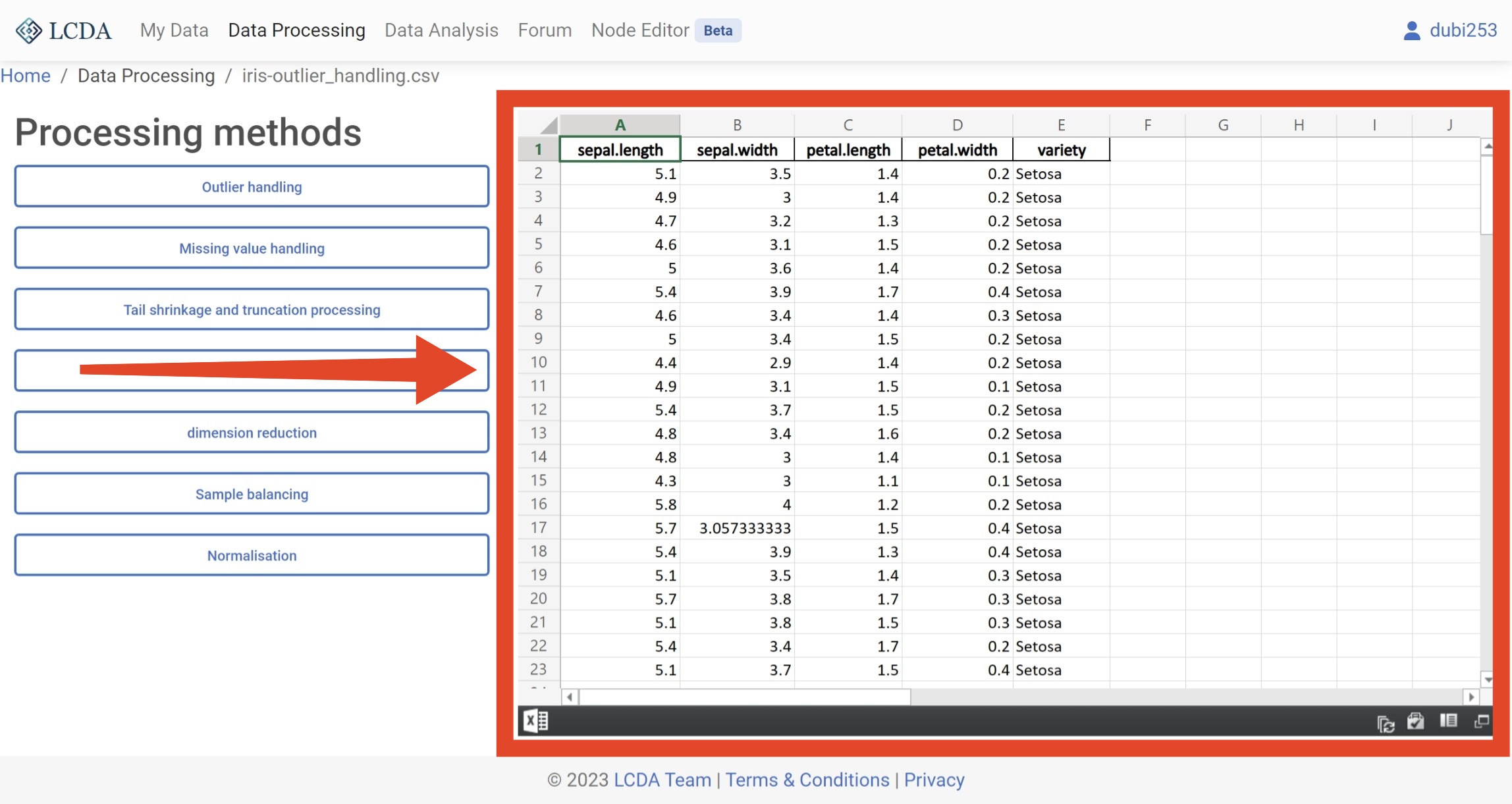
同时,新的数据集也会被保存到您的数据集中。您可以通过访问
My Data页面来查看或下载您新的数据集。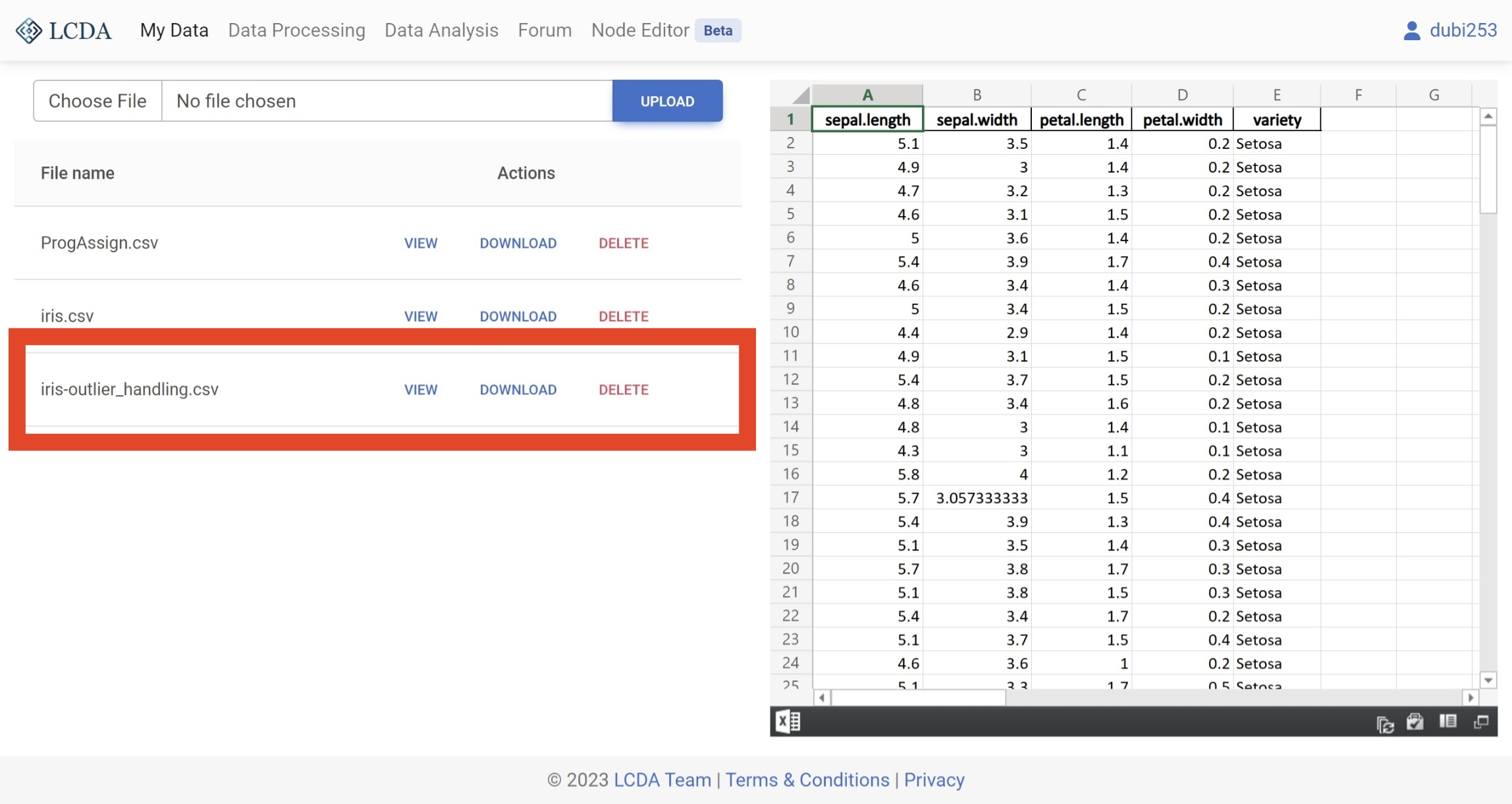
数据处理算法介绍
异常值处理(Outlier handling)
算法描述
异常值处理算法用于识别和处理数据集中的异常值。在统计学中,异常值是指明显不同于其他观测值的数据点,可能是由实验误差或其他因素引起的。异常值可能会在统计分析中引起严重问题,并影响结果的准确性和可靠性。因此,异常值处理算法对于识别和处理这些问题数据点至关重要。这些算法可以帮助提高数据集的质量,并最终导致更准确和可靠的分析结果。
异常值处理算法可以采用多种方法进行识别和处理,包括基于统计学的方法、基于机器学习的方法和基于深度学习的方法等。常用的统计学方法包括3σ原则、箱线图法等;基于机器学习的方法包括局部离群点因子(LOF)、孤立森林(Isolation Forest)等;而基于深度学习的方法则包括自编码器(Autoencoder)等。
在处理异常值时,需要根据具体情况选择合适的算法。有时,一些异常值可能包含有用的信息,因此需要进行仔细的考虑和处理。总的来说,通过合适的异常值处理算法,可以提高数据集的质量和结果的准确性。
算法参数
Detection method:异常值检测方法。目前支持 3-sigma, IQR, 和 MAD 三种方法。Peocessing method:异常值处理方法。目前支持set to null,set to mean, 和set to median三种方法。
算法示例
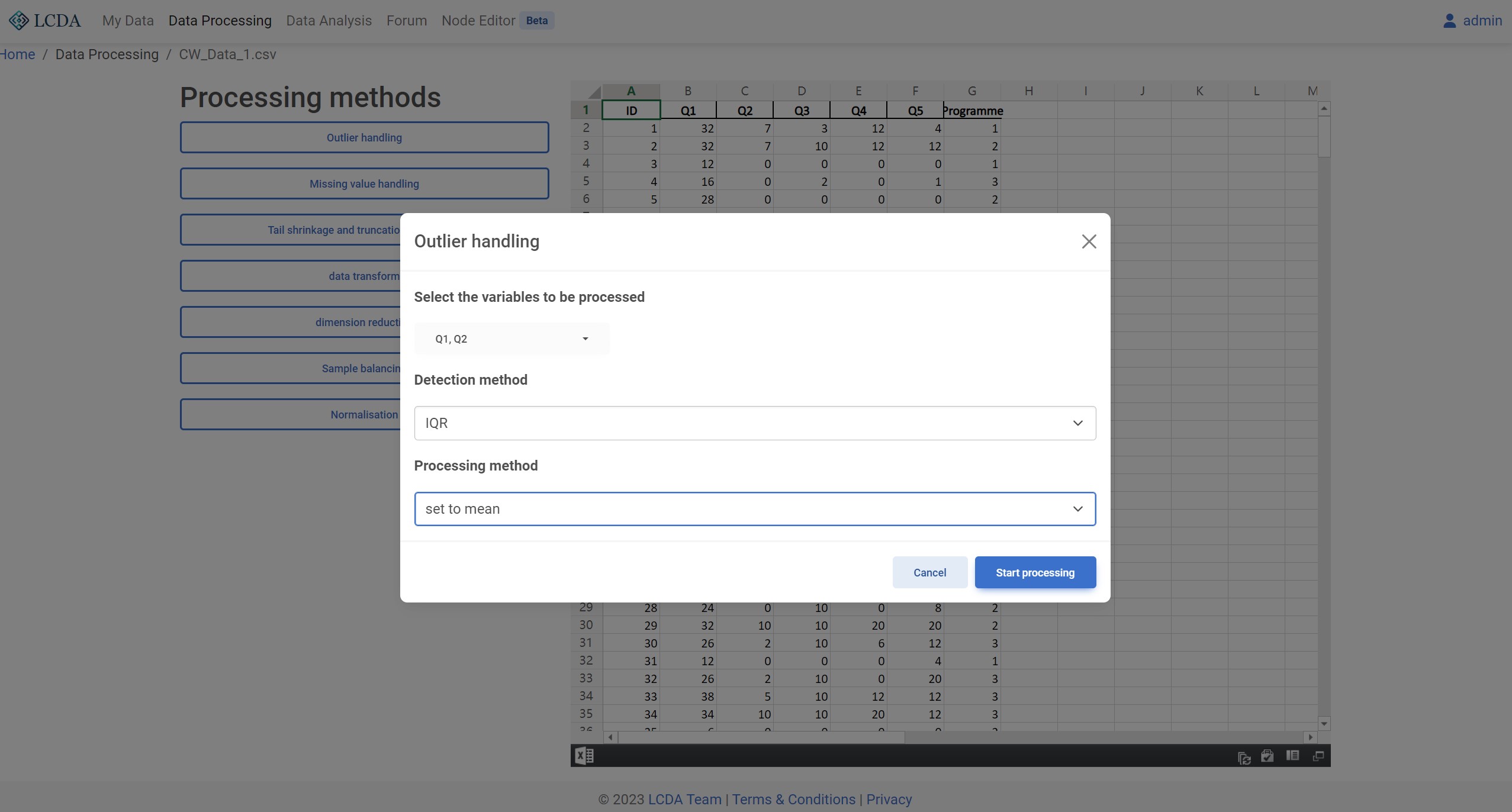
缺失值处理(Missing value handling)
算法描述
缺失值处理是指对数据集中存在的缺失值进行处理的过程。在数据分析和机器学习任务中,缺失值是常见的问题。缺失值的存在可能是由于数据收集过程中的错误、人为遗漏或者其他因素导致的。如果不对缺失值进行处理,将会影响数据分析和机器学习模型的准确性和可靠性。
缺失值处理的方法包括删除、插补和预测等。删除是指直接将包含缺失值的数据行或列删除。这种方法可能会导致数据量减少,但可能会使数据集变得不完整,丢失有用的信息。插补是指使用已有的数据来推断缺失值。插补方法包括均值插补、中位数插补、回归插补和插值法等。预测是指使用机器学习模型来预测缺失值。这种方法需要先用已有数据训练机器学习模型,然后使用该模型来预测缺失值。
在选择缺失值处理方法时,需要考虑数据的性质、数据缺失的原因以及处理方法可能引入的偏差等因素。通过合适的缺失值处理方法,可以提高数据分析和机器学习模型的准确性和可靠性。
算法参数
identification method:缺失值检测方法。目前支持empty,space,None和Non-numeric四种方法。filling method:缺失值处理方法。目前支持mean,median, 和mode三种方法。
算法示例
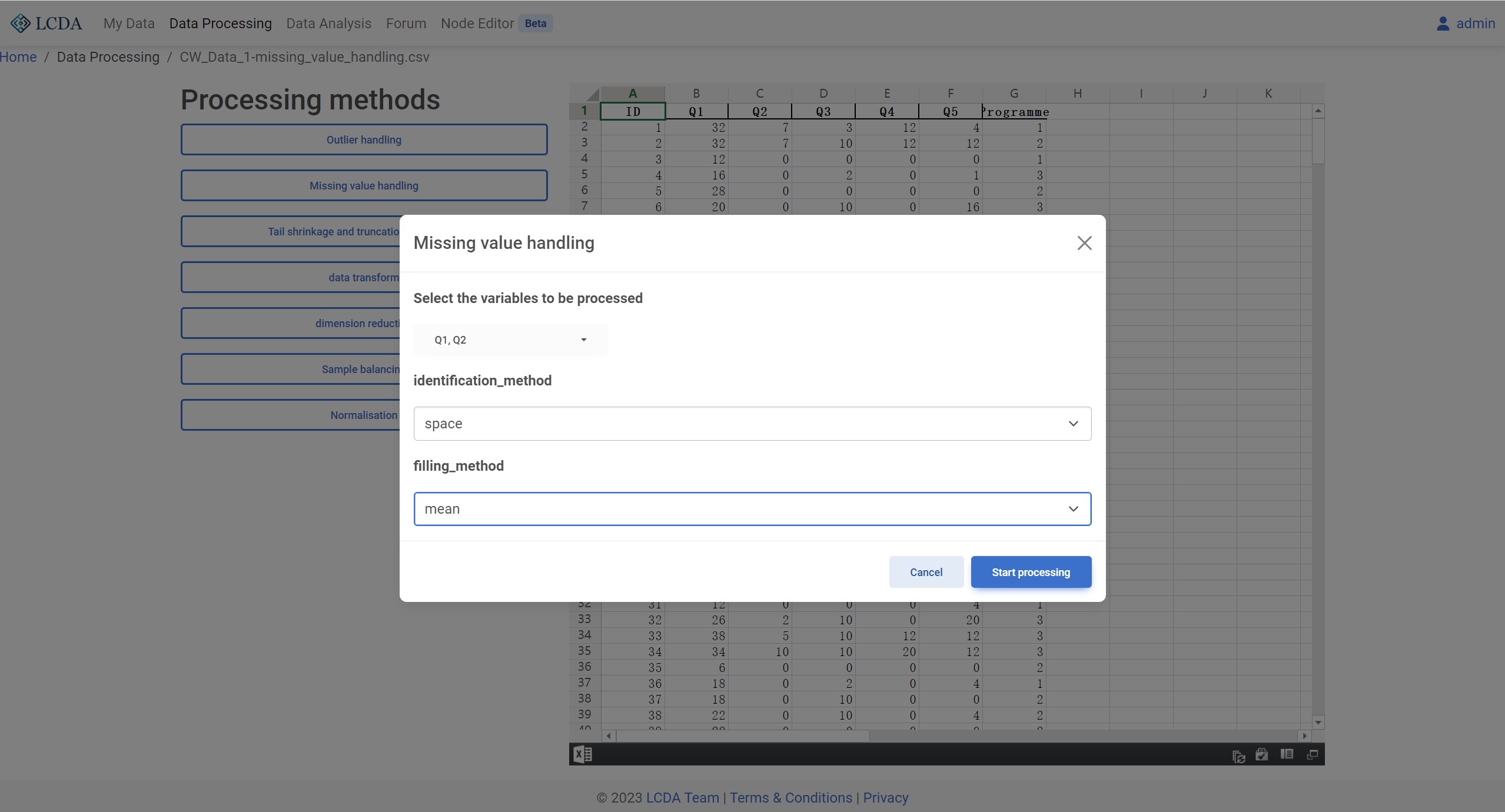
缩尾截尾处理(Tail shrinkage and truncation processing)
算法描述
样本数据足够多时为了剔除一些极端值对研究的影响,一般会对连续变量进行缩尾/截尾处理。缩尾截尾处理的目的是使数据集中的极端值更加接近于中心值,从而使得数据集更加符合正态分布。会在从小到大排列后,处理超出变量特定百分位范围的数值,标准为低于下限和超出上限。缩尾是替换为其特定百分位数值,截尾是直接删除值。
算法参数
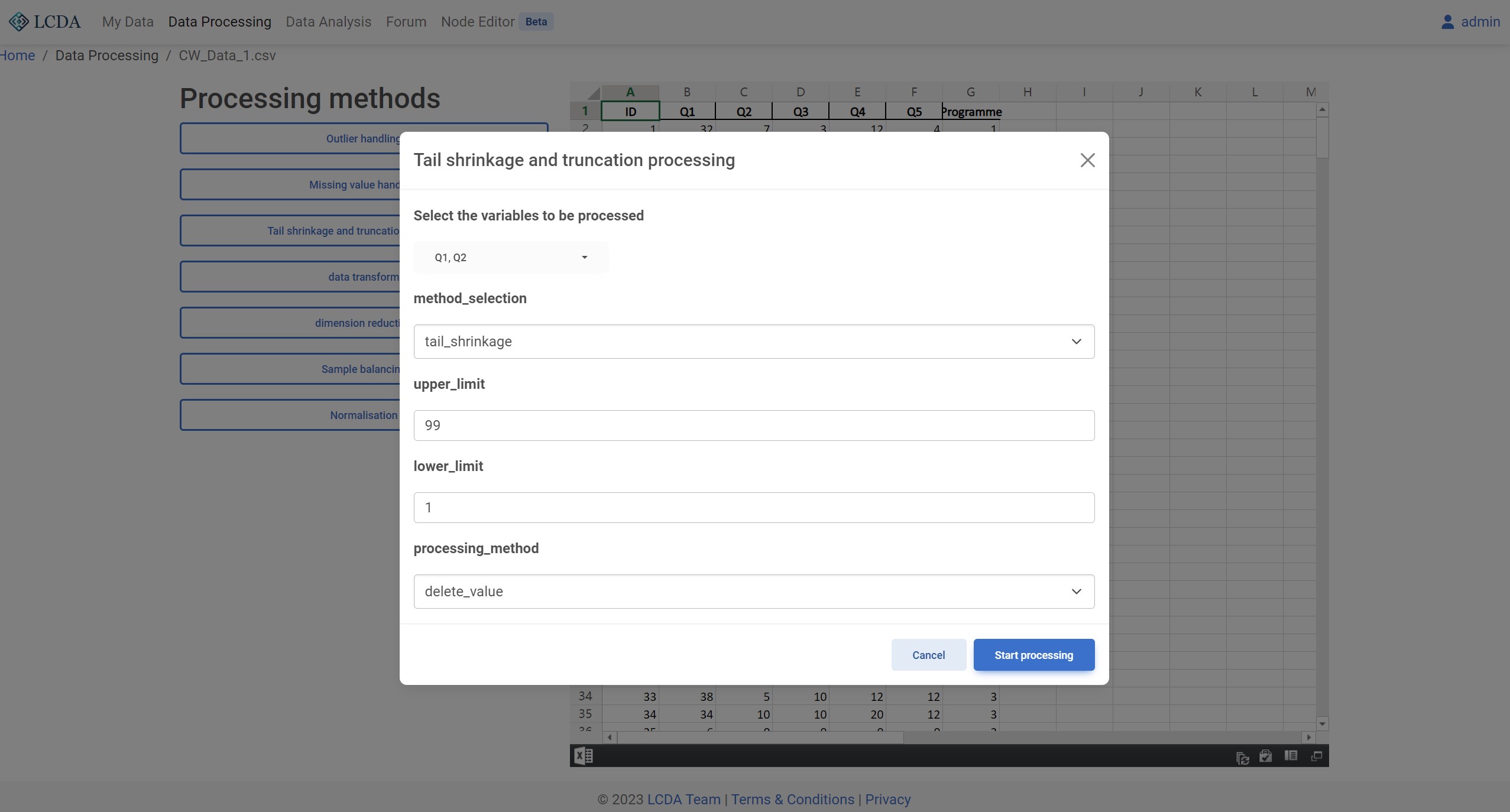
method_selection:缩尾截尾处理方法。目前支持tail_shrinkage和tail_truncation两种方法。upper_limit:缩尾截尾处理的上限。类型为数值。lower_limit:缩尾截尾处理的下限。类型为数值。processing_method:缩尾截尾处理方法。目前支持delete_value和delete_row两种方法。
算法示例
数据转换 (Data transformation)
算法描述
数据变换是指将通过替换/将数据从一种表示形式转换为另一种表示形式,以提取或改变其中的信息或特征。在数据分析和机器学习领域中,数据变换是数据预处理的一个重要步骤,可以用于数据降维、特征提取、异常检测、数据平滑等多种任务。
算法参数
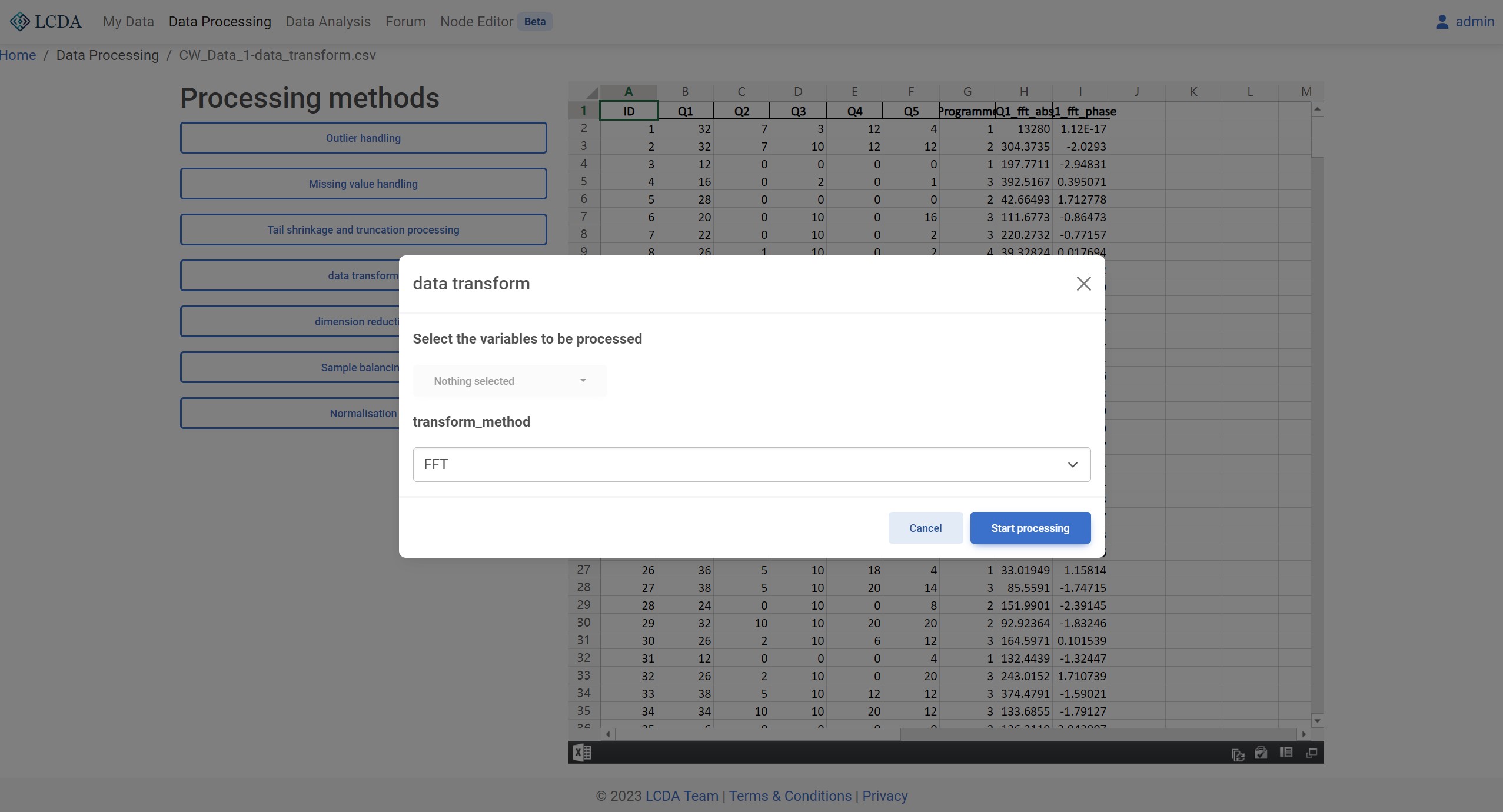
transform_method:数据转换方法。目前支持 FFT 和 IFFT (Inverse Fast Fourier Transform) 两种方法。
算法示例
数据降维 (Dimension reduction)
算法描述
数据降维是指将高维度数据集中的数据映射到低维度空间中,同时尽可能地保留原始数据集的特征信息。在数据分析和机器学习领域中,高维数据集的存在经常会导致计算复杂度的大幅增加,同时也会使得数据的可视化和解释性变得困难。因此,数据降维可以有效地减少数据集的维度,提高数据的处理效率和可解释性,同时也能够降低过拟合的风险,提高机器学习模型的泛化能力。
算法参数
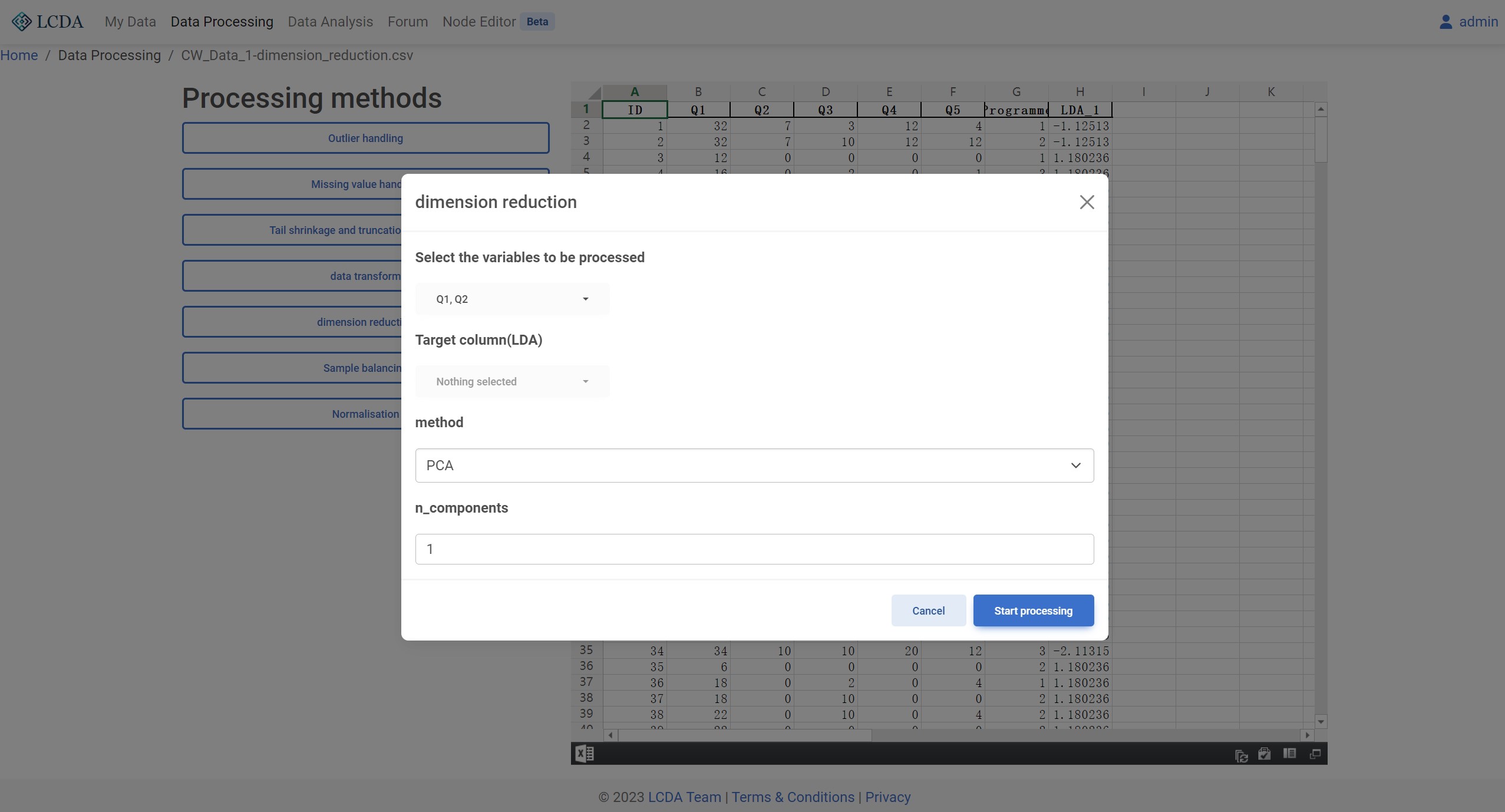
method:数据降维方法。目前支持 PCA 和 LDA 两种方法。n_components:主成分数。类型为数值。当method为PCA时,n_components为主成分数。当method为LDA时,n_components为线性判别数。
算法示例
样本均衡(Sample balancing)
算法描述
样本平衡是指对数据集中的样本进行调整,使得各个类别的样本数量尽可能地均衡分布。在机器学习和数据分析中,样本平衡是一个重要的预处理步骤。这是因为当数据集中某些类别的样本数量比其他类别的样本数量要多很多时,会导致模型的训练和预测结果存在偏差,影响模型的性能和准确性。
样本平衡可以通过多种方法来实现,比如下采样、过采样、合成样本等。下采样是指从样本数量较多的类别中随机地去除一些样本,使得样本数量与其他类别相当。过采样是指通过对样本数量较少的类别进行复制或合成新的样本来增加该类别的样本数量。合成样本是指使用生成模型(如SMOTEENN)生成新的样本数据,从而增加样本数量并使不同类别的样本数量更加均衡。
样本平衡可以提高模型的性能和准确性,并降低由于样本不平衡带来的偏差。但是,过度的样本平衡也可能会导致过拟合问题,因此需要根据具体情况进行调整和平衡。
算法参数
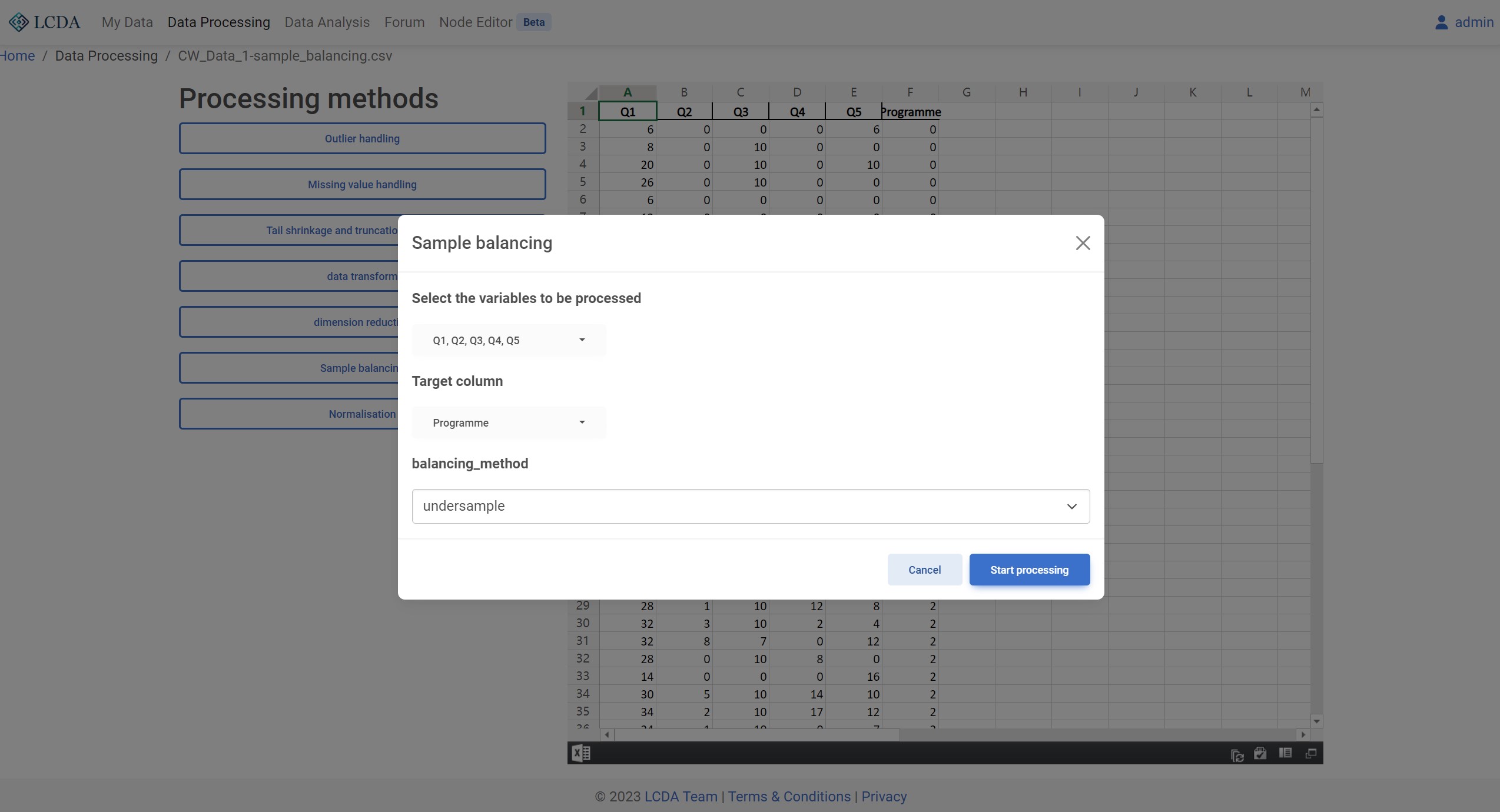
balancing_method:样本均衡方法。目前支持undersample(RandomUnderSampler),oversample(RandomOverSampler) 和combined(SMOTEENN )三种方法。
算法示例
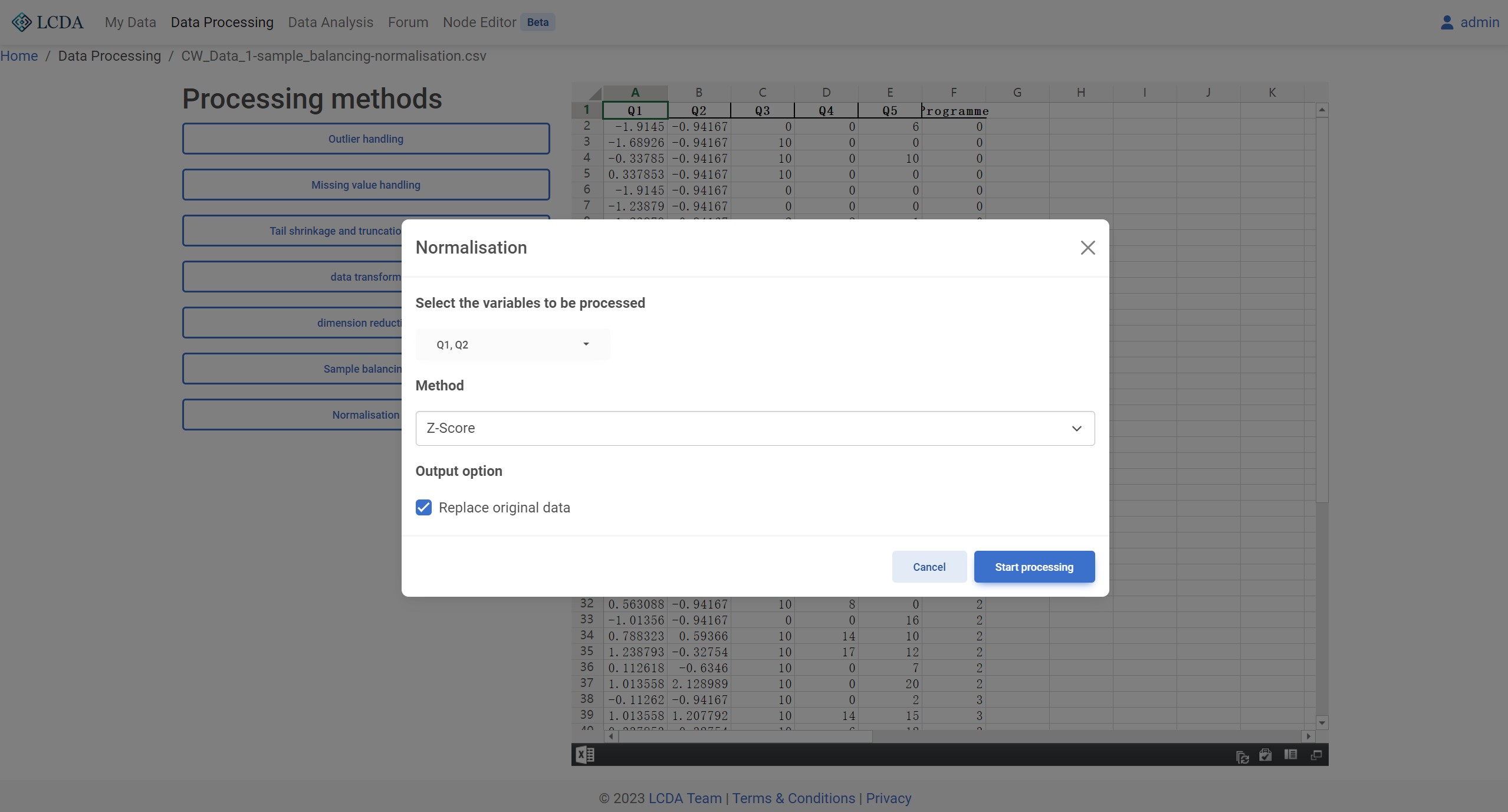
标准化(Normalization)
算法描述
数据标准化是指对原始数据进行处理,使其符合一定的标准或规范,以便于进行比较和分析。数据标准化常见的方法是将数据转换为均值为0,方差为1的标准正态分布或将数据缩放到一定的范围内。
数据标准化的主要目的是消除数据中的单位差异和数量级差异,从而使得不同变量之间的比较更加公平。例如,如果两个变量的数值范围相差很大,那么它们之间的比较可能会受到较大的误差。通过对数据进行标准化,可以消除这种误差,使得数据更加可靠和可解释。
数据标准化在许多数据分析和机器学习任务中都是必要的步骤,例如聚类分析、回归分析、神经网络等。常用的数据标准化方法包括z-score标准化、min-max标准化、均值方差归一化等。
算法参数
算法示例